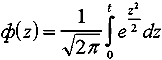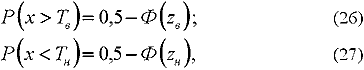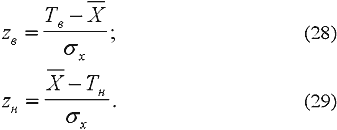|
  8-800-777-16-36 - звонок бесплатный
|
ООО "СтройМеханика" |
||||||||||||
 |
|
|||||||||||||
| статьи | сайты | |||||||||||||
|
ПРИЛОЖЕНИЕ 8
СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ТЕХНОЛОГИЧЕСКОГО КОНТРОЛЯДля статистической обработки результатов технологического контроля из лабораторного журнала выбирают нес результаты, полученные в контрольный период (месяц, квартал, год). Минимальный объем выборки, пригодный для статистического анализа, должен содержать не менее 30 результатов. Не разрешается исключать из выборки те результаты, которые выходят за границы поля допусков. Точность технологических процессов оценивают путем сравнения среднеарифметических значений Xср контролируемых параметров по пп. 10.2 и 10.3 настоящей Инструкции, вычисленных по данным производственного контроля с нормируемыми значениями Сx. Если отклонение Xср от Сx, выраженное в % от Сx, превышает базовые, величины, указанные в таблице 12, то такие процессы и параметры нуждаются в корректировке и уточнении. Стабильность технологических процессов оценивают по величине коэффициентов вариации (Vx) контролируемых параметров и по количеству результатов, выходящих за пределы поля допусков (Тв и Тн). Если фактические значения Vx превышают нормируемые показатели (табл. 12), а количество результатов, выходящих за пределы поля допусков более 5%, то это означает, что технологический процесс неустойчив и необходимо принять меры для его стабилизации. Статистические характеристики определяют по формулам:
среднеквадратичное отклонение - σх
коэффициент вариации - Vx
При большом объеме выборки обработку результатов текущего контроля следует начинать с составления вариационной табл. 18. Ширину интервалов h следует выбирать такой, чтобы число интервалов K было не менее 7 и не более 13. При объеме выборки менее 50 результатов число интервалов следует принять 7 при N = 1000, K = 13. Ширину интервалов h определяют путем деления величины размаха (xmax-xmin) на число принятых интервалов K и полученный результат округляют. Для каждого интервала определяют численное значение интервала U. Таблица 18
Все результаты, записанные в журнале текущего контроля в течение анализируемого периода времени, должны быть разнесены по интервалам табл. 18. Пометки следует записывать в виде точек и черточек. Вычисление числовых характеристик следует проводить в табличной форме. Для этого определяют условные центры каждого интервала (е) по формуле
где U - значение центра интервала;
За условный центр рассеивания а принимают то значение центра интервала (U), для которого абсолютная частота т наибольшая и располагается ближе к середине интервального ряда. Статистические характеристики для интервального ряда распределения определяют по формулам:
б) дисперсия
в) среднеквадратическое отклонение Таблица 19
Таблица значений функций
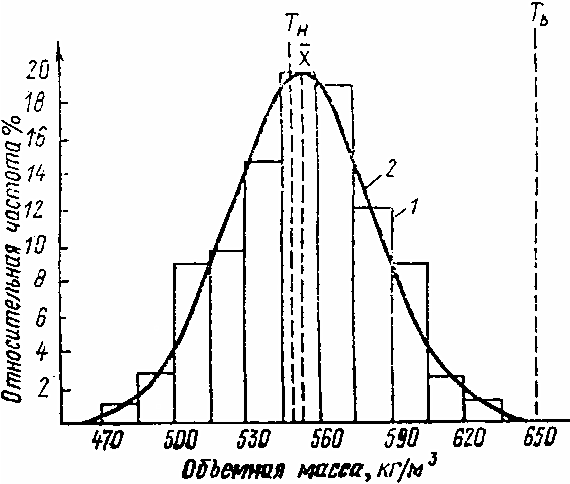
Для большей наглядности характера распределения изучаемого параметра вариационный ряд следует изобразить в виде графика (рис. 2), для чего определяется повторяемость результатов (частотность) в каждом интервале f, выраженная в процентах (графа 5 табл. 18). Частотность определяется по формуле
На гистограмме отмечаются также границы поля допусков Тн и Тв. Доля брака определяется по формулам и с помощью табл. 19:
где Р (х > Тв) - доля брака, у которого контролируемый параметр выше Тв;
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © 2004-2017 ООО "СтройМеханика" |
каталог
прайс-лист
бизнес-план
о нас
контакты
статьи
|
||

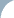




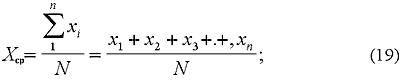
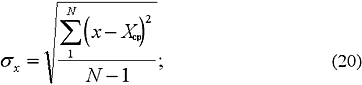



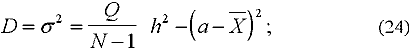
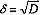 ;
;